이게 뭐야?

트리 종류 중에 하나이며, 연속된 구간(특정 범위)의 합(최솟값, 최댓값, 곱 등)을 구하는데 많이 쓰인다.

아래에서 선형구현과 비교하며 왜 쓰는지, 어떻게 사용하는지 gif를 준비해 놨으니 자세히 알아보자.

세그먼트 트리 문제 보기

문제 - 1 페이지

www.acmicpc.net

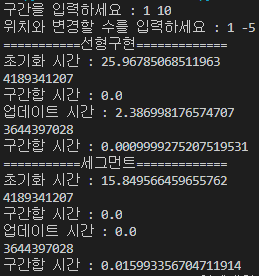
일단 결과부터 보자

입력된 수는 10의 7제곱이다.

10개의 데이터 [ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ]를 두고 구간 합을 구해본다.

예시 입력 : 1 10

예시 출력 : 55

선형 구현 O(N)

초기화 과정 O(N)

ARRAY = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
for i in range(1,len(ARRAY)):
	ARRAY[i] += ARRAY[i-1]

좌측의 데이터에 현재의 데이터를 더해가면서 구간 합 배열을 생성한다.

출력 과정 O(1)

예시 입력처럼 특정 구간이 입력되면 해당 구간의 합을 출력한다.

이미 초기화 과정에서 모든 합을 구해 놨기에 ARRAY[e-1]-ARRAY[s-2]를 수행하면 해당 구간 만큼의 값이 O(1)에 출력된다.

세그먼트 트리 구현 O(logN)

사람들마다 구현하는 스타일이 조금씩 다른데, 본인이 편한 방법으로 수정해서 사용하면 된다.

초기화 과정 O(logN)

def init(start, end, index):
    if start==end: #가장 끝에 도달 했으면 ARRAY를 삽입
    	tree[index] = ARRAY[start]
    	return tree[index]
    mid = (start+end)//2
    tree[index] = init(start,mid,index*2)+init(mid+1,end,index*2+1)
    #좌측 노드와 우측 노드를 합한다

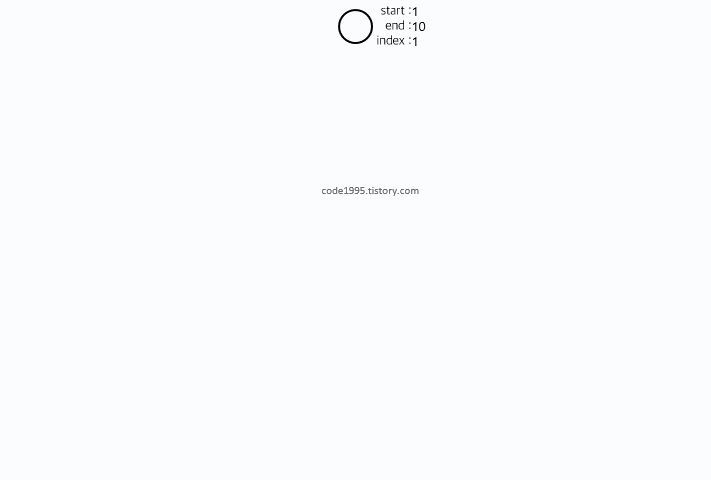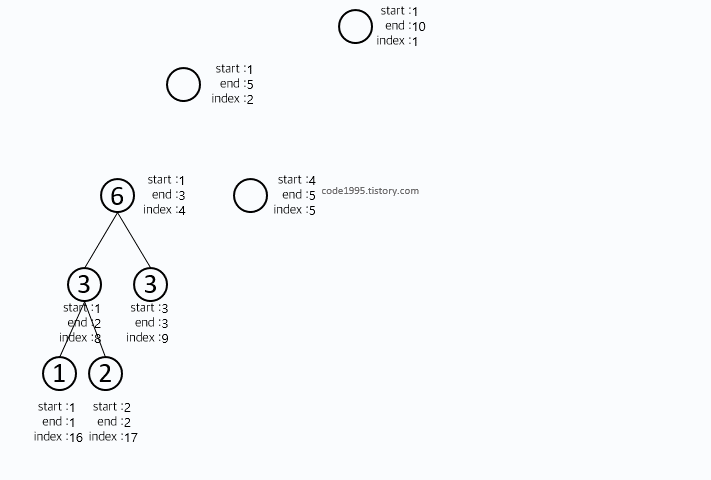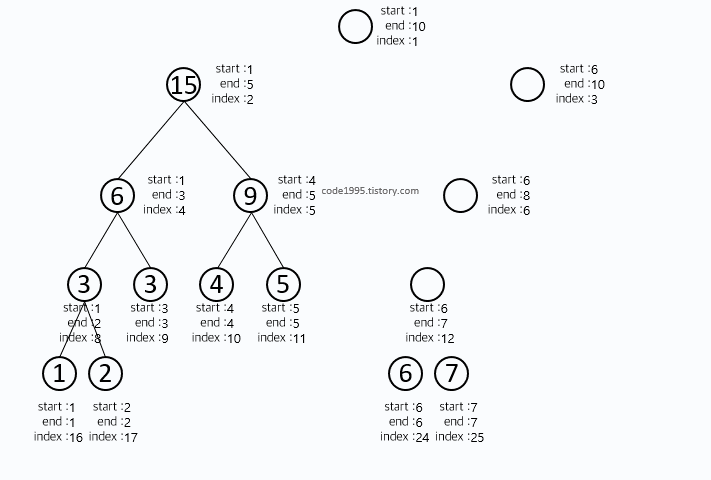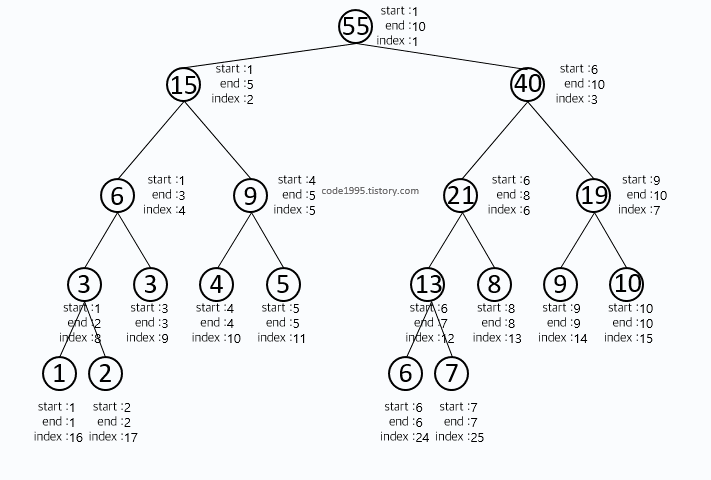
재귀적으로 구현했으며, start와 end가 같아지는 순간에 ARRAY에 있는 값을 tree에 넣어 준다는 것을 눈여겨 봐야한다.

또한 재귀적으로 현재 인덱스에 좌측과 우측 자식노드의 값을 더해주게 된다.

그림을 봐도 이해가 안된다면 직접 손으로 그려가는 것을 추천한다.

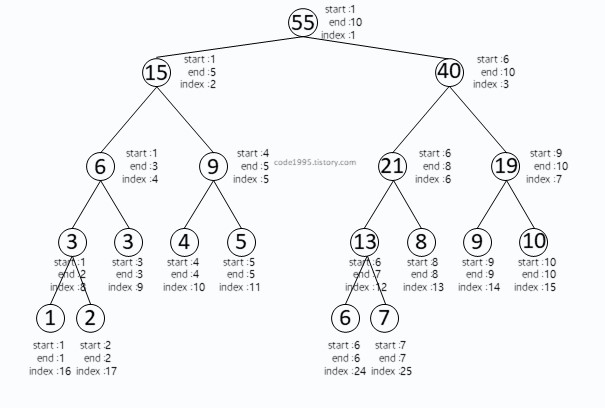
출력 과정 O(logN)

초기화 함수와 매우 유사하다. 하지만 구간 합만 반환하면 되기 때문에 값의 변경은 없다는 점을 기억하자.

def query(start,end,index,qLeft,qRight):
    #범위를 벗어나는 경우
    if qLeft>end or qRight<start:
    	return 0
    #범위 내에 있는 경우
    if qLeft <= start and end<=qRight:
    	return tree[index]
    mid = (start+end)//2
    return query(start,mid,index*2,qLeft,qRight)+query(mid+1,end,index*2+1,qLeft,qRight)

최종 소스코드

N = 10
ARRAY = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
tree = [0]*(N*4)

def init(start, end, index):
    if start==end: #가장 끝에 도달 했으면 ARRAY를 삽입
    	tree[index] = ARRAY[start]
    	return tree[index]
    mid = (start+end)//2
    tree[index] = init(start,mid,index*2)+init(mid+1,end,index*2+1)
    #좌측 노드와 우측 노드를 합한다
    
def query(start,end,index,qLeft,qRight):
    #범위를 벗어나는 경우
    if qLeft>end or qRight<start:
    	return 0
    #범위 내에 있는 경우
    if qLeft <= start and end<=qRight:
    	return tree[index]
    mid = (start+end)//2
    return query(start,mid,index*2,qLeft,qRight)+query(mid+1,end,index*2+1,qLeft,qRight)
    
init(1,N,1)	#부모 노드 인덱스(1)부터 시작
s,e = map(int,input().split())
print(query(1,N,1,s,e))#s~e 구간합 출력

이후, 업데이트 함수는 Fenwick Tree(BIT)와 함께 다뤄 포스팅 할 예정이다.

저작자표시 비영리 변경금지